What is the Golden Ratio?
The golden ratio or golden mean, represented by the Greek letter phi (ϕ), is an irrational number that approximately equals 1.618. The golden ratio results when the ratio of two numbers is the same as the ratio of their sum to the larger of the two numbers. In other words, the golden ratio occurs when you divide a line segment into two smaller segments of different lengths for which the ratio of the whole line segment to the longer segment is equal to the ratio of the longer segment to the shorter segment.
A Brief History of the Golden Ratio
The golden ratio is a special number, and its story begins with the ancient greeks.
1. 300 BC: Greek mathematician Euclid provided the first written definition of the golden ratio in his math textbook Elements. At the time, Euclid called it the “extreme and mean ratio.”
2. 1509 AD: Italian mathematician Luca Paciolifurther used the golden proportion to describe the natural world in his book De Divina Proportione (On the Divine Proportion), which was illustrated by Leonardo da Vinci.
3. 1835: German mathematician Martin Ohm first described the ratio as “golden” when he used the term goldener schnitt, which translates to “golden section.”
4. 1910: American mathematician Mark Barr first used the Greek letter phi (ϕ) to represent the golden ratio.
How to Calculate the Golden Ratio
The golden ratio occurs when you take a line segment and divide it into two smaller segments of different lengths where the ratio of the whole line segment to the longer segment is equal to the ratio of the longer segment to the shorter segment. Two quantities a and b have a golden ratio relationship if
where a > b > 0 and the Greek letter phi (ϕ) represents the golden ratio. The golden ratio expressed numerically is
Since the number phi is irrational, the digits after the decimal point continue on forever without repeating.
Golden Ratio and the Fibonacci Sequence
The golden ratio is closely connected to the Fibonacci sequence. This is because as the Fibonacci numbers increase, the ratio of any two consecutive Fibonacci numbers gets closer and closer to the golden ratio.
The Golden Ratio in the Real World
The below examples of the golden ratio are exceptions rather than rules—in general, claims that the golden ratio appears throughout art, architecture, nature, and the human body are overstated. However, the golden ratio does feature prominently in a few natural and manmade examples.
- In plants: You can find the golden ratio in the spiral arrangement of leaves (called a phyllotaxis) on some plants, or in the golden spiral pattern of pinecones, cauliflower, pineapples, and the arrangement of seeds in sunflowers.
- In art: Within the last century, artists have been inspired by the aesthetics of the golden ratio and incorporated it into their works. For example, the canvas of surrealist painter Salvador Dali’s The Sacrament of the Last Supper is a golden rectangle, and the painting itself features a giant dodecahedron with edges in the golden ratio.
- In architecture: The Parthenon in Greece incorporates the golden ratio in many of its design elements. In the twentieth century, Swiss architect Le Corbusier used the golden ratio in his Modulor system for the scale of architectural proportion. The United Nations Secretariat Building in New York City was designed using the golden ratio: the size and shape of the windows, columns, and some sections of the building are based on the golden ratio.


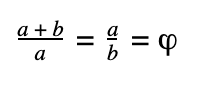
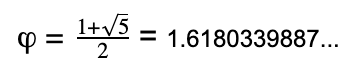

 Users Today : 11
Users Today : 11 Total views : 666874
Total views : 666874